题目分析
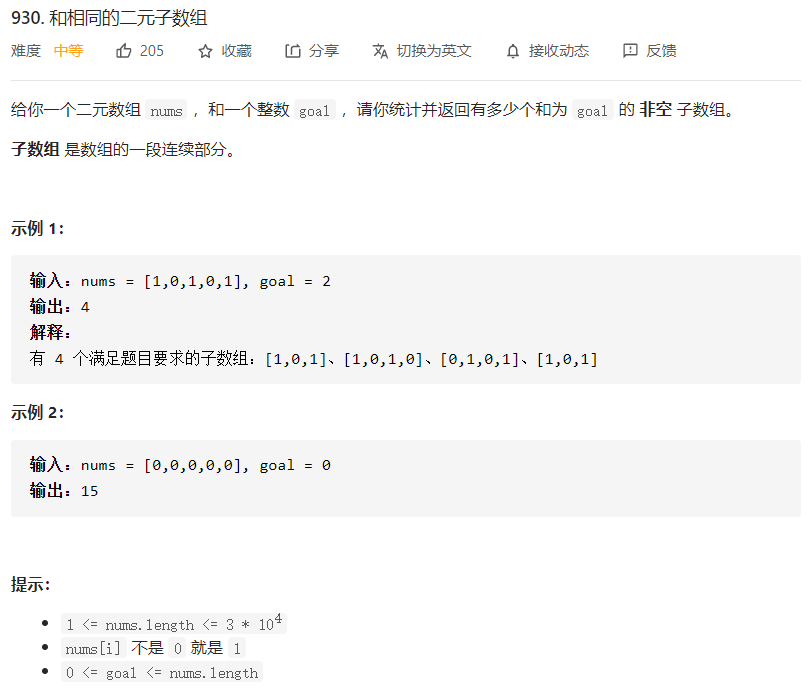
本题是连续子数组求和问题,子数组求和往往需要用到前缀和,因此可以使用sums记录前缀和,然后遍历起始和终止位置即可。这是本题的一般解法,时间复杂度为$O(n^2)$,空间复杂度为$O(n)$。但是有没有更精妙的解法呢?给小伙伴们提示一下,可以观察leetcode入坑题即第一题两数之和。
哈希表
前缀和sums[k]表示从索引0到索引k的元素之和,那么子数组i到j的元素之和是否可以表示为sums[k] - sums[i - 1]呢?因此即求前缀和数组中两数之差为goal的个数。
使用哈希表dic记录前缀和出现的次数,假设当前索引为j,前缀和为m,满足从i到j的元素之和为goal的子数组个数为dic[m - goal]。
算法的时间复杂度为$O(n)$,空间复杂度为$O(n)$
下面是Java语言的题解
1 | class Solution { |
下面是Kotlin语言的题解
1 | class Solution { |
刷题总结
本题的数据只有0和1,还可以使用滑动窗口进行求解,因为不是通用的解法,因此这里不做过多介绍。想了解的小伙伴们可以取力扣官网查看本题题解。